Burette & pipette - calibration of volumetric glassware used in titrations
Ability to precisely measure volume of the solution is crucial for the accuracy of chemical analysis. Volumetric glass - while made according to known standards - is never perfect. Using A class pipette we can safely assume its volume falls inside of the range given by the standard specification, but it is still a range and differences between individual pipettes can be large. For example, according to ASTM E287-02 tolerance for the 10 mL A class pipette is 0.020 mL. That means that both 9.98 mL and 10.02 mL pipettes are both good enough to be classified as A class, but the difference between their volumes is 0.4%.
To minimalize problems we can calibrate the glass - that is, measure the real volume of solution delivered or contained - by weighing mass of the water. Weighing can be done with very good accuracy, and knowing water density we can calculate volume of the given water mass. Thus we can determine exact capacity of the glassware. Well, perhaps not the exact capacity, but at least we will know the volume with much higher accuracy than if we assume its nominal value.
To calibrate the glass we need a good analytical balance, and distilled (or DI) water of known temperature. To be sure measurements are correct it is a good idea to keep water, balance and calibrated glassware in the same room long enough to be sure everything have the same temperature. Room doesn't have to be thermostated, although temperature should not change during the calibration process. It also won't hurt to calibrate the glass in the temperature similar to the temperature in which it will be used, to minimalize later effects of the glass and water thermal expansion.
Mass of the water can be converted to the volume using equation
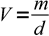 1
1where V is a volume, m is a mass of water and d is density of water in the given temperature. Density of water is listed in the table:
| temperature °C | density g mL-1 |
|---|---|
| 15 | 0.99913 |
| 16 | 0.99897 |
| 17 | 0.99880 |
| 18 | 0.99862 |
| 19 | 0.99843 |
| 20 | 0.99823 |
| 21 | 0.99802 |
| 22 | 0.99780 |
| 23 | 0.99757 |
| 24 | 0.99733 |
| 25 | 0.99707 |
| 26 | 0.99681 |
(taken from the International Critical Tables of Numerical Data, Physics, Chemistry and Technology, vol. III)
Calibration of volumetric flasks
Weigh empty, dry flask. Fill it with distilled water to mark. Weigh again. Mass difference is the mass of water. Repeat 3-4 times.
Calibration of single volume pipettes
Weigh empty, dry, closed weighing bottle. Pipette water into the bottle, close, weigh again. Mass difference is the mass of water. Repeat 3-4 times.
In both cases use your results to calculate average mass.
Quite often single volume pipette and volumetric flask are used together - diluted sample is pipetted from the flask to carry on separate titrations. To calculate sample size we have to multiply titration result by the ratio of the flask volume and pipette volume. Instead of using each time volumes of the pipette and flask it is easier and faster to use so called commensurability of the flask and pipette - just divide flask volume by the pipette volume and use this number to calculate original sample size.
Calibration of burettes
Burettes can be not only wrong (within allowed tolerance), but the error can depend on the volume delivered. Thus we will need not a single number, but either a table or a plot of corrections. To prepare it, repeat the same procedure for each multiply of 5.00 mL (5.00 mL, 10.00 mL, 15.00 mL...):
- Weigh empty, closed weighing bottle.
- Use burette to transfer water to the weighing bottle, starting from 0.00 mL.
- Close and weigh.
Collected data can be used to prepare burette volume corrections curve:
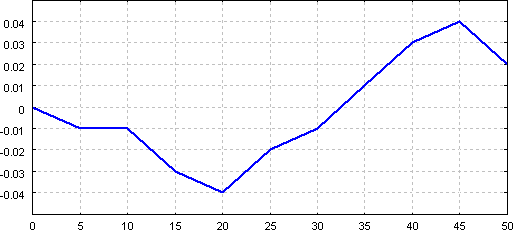
which allows easy checking of a correction for a volume read from the burette.
Graduated pipettes and cylinders can be also calibrated, but as they are usually used to measure volumes of auxiliary substances (with relatively wide range of acceptable concentration) their accuracy is not that important.
Volumes measured will always depend on the temperature. However, there is no simple and easy way to deal with the temperature corrections. First, thermal expansion coefficient depends on the solute and its concentration. Second, glass expands as well - and not surprisingly different types of glass have different expansion coefficients. That means that each solution in each type of glass have slightly different temperature corrections for volume. Thus for precise work it is advisable to not use some general corrections, but to calibrate the glassware again, for different temperature.
We should also correct our results for the air buoyancy. To get exact weights we should weigh glass and solutions in vacuum, but we weigh them in air. Weights used on the balance have much higher density than water solution, so their volume is much lower - and they differ in buoyancy. Ignoring this effect induces errors of similar magnitude as ignoring termal expansion in normal lab conditions (that is, temperatures differing by several degrees between titrations).
Let's compare results of the weighing 1.000 L of water using brass weights in vacuum and in air at the Earth surface. We will assume brass density to be 8.500 g/mL, air density to be 1.204 g/L (or 1.204×10-3 g/mL) and water density to be 0.9982 g/mL.
To balance the balance in vacuum we have to put 1 kg of water and 1 kg of brass on the scales. That means 1000 g:0.9982 g/mL=1002 mL (1.002 L) of water, and 1000 g:8.500 g/mL=117.6 mL (0.1176 L) of brass.
In the air - due to buoyance - apparent weight of both brass and water is smaller - in each case by the weight of the displaced air. Apparent weight of water will be 1000 g - 1.002 L×1.204 g/L = 998.8 g. To balance it we will need Vbrass mL of brass, this volume can be calculated from the 998.8 g = Vbrass×dbrass - Vbrass×dair = Vbrass(dbrass - dair). Plugging all numbers in we arrive at Vbrass = 117.5 mL. That's the volume of the brass weights that we have to put on the scale. Reading their markings we will arrive at conclusion that water weights 998.9 g. This is 1.1 g less than in vaccum - and that means 0.11% error in volume determination.
After correct calibration class B glassware can be used to perform analysis with the same accuracy as class A glassware. However, B class glassware is usually of lower quality, so we may expect higher thermal expansion coefficients and lower resistance to chemicals. That in turn means we have to be more accurate in our work and pay more attention for changing conditions.




