Acid base titration - equivalence point pH calculation

Remember, that what we calculate is not the pH at the end point - but the theoretical pH at the equivalence point.

In the equivalence point we have solution containing pure salt that is a product of the neutralization reaction occurring during titration. Thus calculation of the equivalence point pH is identical with the calculation of the pH of the salt solution.

Depending on the type of titration there are at least three different cases to discuss.

In the case of titration of strong acid with strong base (or strong base with strong acid) there is no hydrolysis and solution pH is neutral - 7.00 (at 25°C).

In the case of titration of weak acid with strong base, pH at the equivalence point is determined by the weak acid salt hydrolysis. That means we have to find pK_b of conjugated base and calculate concentration of OH^- starting from there, then use pH=14-pOH formula. See pH of weak acids and bases lecture and pH cheat sheet for details of calculation.

In the case of titration of weak base with strong acid, situation is very similar - pH at the equivalence point is determined by the weak base salt hydrolysis. Thus we need pK_a of conjugated acid to calculate H⁺ and pH. Check lecture and cheat sheet mentioned above for details.

In the case of polyprotic acids and bases calculations get much harder. You may try to follow methods described in the lecture on polyprotic acids and bases pH calculation, or you may use BATE - pH calculator.

Calculate pH at the equivalence point of formic acid titration with NaOH, assuming both titrant and titrated acid concentrations are 0.1 M. pK_a = 3.75.

At the equivalence point we have a solution of sodium formate. As both concentrations of titrated acid and titrant are identical, and monoprotic formic acid reacts 1:1 with sodium hydroxide, we have to add identical volume of base to the given volume of acid. That in turn means that final volume is twice that of initial volume of acid sample, so after dilution concentration of formate must be half that of acid - that is 0.05 M.

We have titrated weak acid, so to calculate pH we have to calculate concentration of OH^- from formate hydrolysis first. Formate is a weak base with

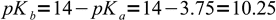1

Let's try to use the most simplified formula first:

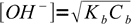2

Using 10^-10.25 and 0.05 we get

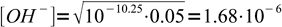3

To be sure we can use the simplified formula we have to check, whether hydrolysis was below 5%. To do so, we should divide concentration of OH^- by initial concentration of formate. That means

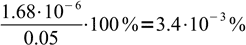4

Obviously assumption about low hydrolysis degree is correct, and we can proceed with calculation of pOH:

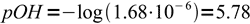5

and pH:

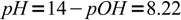6

What is pH at the equivalence point of 0.0211 M H₂SO₄ titrated with 0.01120 M NaOH?

7.0

OK, that was very short answer, now a little bit longer one. This is case of strong acid titrated with strong base, so we expect pH at equivalence point to be that of neutral solution - that is, 7.00. In reality the answer will be slightly different. Three reasons for that. First, sulfuric acid has pK_a1 = -3 (very strong acid) but second dissociation step has pK_a2 = 2.0, so it is much weaker. Still strong, but weak enough so that its hydrolysis can't be ignored, especially in more concentrated solutions. Second, NaOH - while strong base - is much weaker than it is commonly assumed, with pK_b = 0.2 (see pK_b of NaOH in ChemBuddy FAQ for details), so in precise calculations its hydrolysis can't be neglected as well. Finally, there is a reason that we are ignoring in all our examples, but that can't be neglected in the real lab - that is, activity coefficients of all ions involved are not 1 (more on that in ChemBuddy lecture on ionic strength and activity coefficients). If we take all these things into account we can calculate pH of the solution to be 7.05, close enough to 7.0.