Potentiometric titration - equivalence point calculation
Remember, that what we calculate is not the end point - but equivalence point.
To calculate potential at the equivalence point in redox titration, we can use exactly the same approximation we can use in every other titration type - that reaction proceeded almost to the end, so concentrations of products are given by the reaction stoichiometry. However, before solving an example in which we will use this approach, let's try to derive more or less general formula for equivalence point potential
Let's assume the reaction that takes place is
mAARed + mBBOx = mAAOx + mBBRed
where Red and Ox indices denote reduced and oxidized forms. We don't care about charges of these substances, we just assume that the reaction is properly balanced and that numbers of electrons exchanged in half reactions are nA and nB. Note, that this reaction equation is much more general than it may seem - while in many cases there are additional ions and molecules consumed/created, as long as their concentrations can be considered constant (either because they are in huge excess like water, or because they are buffered - like pH) they will simply became part of the formal potential of the half reaction.
For such a reaction, and for equivalence point, we can write two Nernst equations, describing potential of the solution:
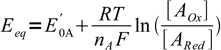 1
1and
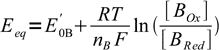 2
2where E'0A and E'0B are formal potentials of both redox systems present.
These equations can be rewritten as
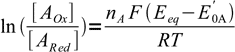 3
3and
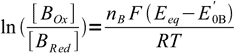 4
4At equivalence point we have mixed stoichiometric amount of ARed and BOx. From the stoichiometry of the reaction we know that
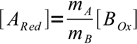 5
5and
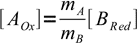 6
6Dividing equations side by side we get
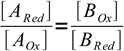 7
7That is in turn equivalent to
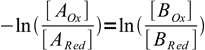 8
8(note sign change, this was done to switch nominator and denominator of the left hand side of the equation).
We are getting close to the final formula. Let's combine above equations:
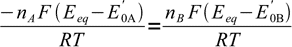 9
9canceling out R, T and F:
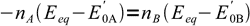 10
10and finally
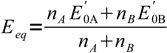 11
11Note, that this equation, although often cited in analytical chemistry books, is not universal. It will work for all reactions that can be described by our skeletal equation. So for example it will work for titration described by the reaction
Fe2+ + Ce4+ → Fe3+ + Ce3+
or even
5Fe2+ + MnO4- + 8H+ → 5Fe3+ + Mn2+ + 4H2O
but not for
Cr2O72- + 6Fe3+ + 14H+ → 6Fe2+ + 2Cr3+ + 7H2O
as in this last reaction stoichiometry coefficient of the Cr2O72-/Cr3+ redox system changes from 1 on the left side of the equation to 2 on the right.
Calculate equivalence point potential if 0.02 M Fe(CN)64- is titrated with 0.1 M Ce4+. E0Ce4+/Ce3+ = 1.61 V, E0Fe(CN)63-/Fe(CN)64- = 0.36 V.
This is a straight application of the formula derived above. In both half reactions one electron is exchanged, so equivalence point potential is given by
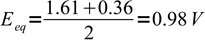 12
12Note, that we can ignore given concentrations of the titrant and titrated substance, as equivalence potential doesn't depend on them.
What is equivalence point potential when 0.1 M I2 solution is titrated with 0.1 M solution of S2O32-. E0I2/I- = 0.535 V, E0S4O62-/S2O32- = 0.08 V.
Reaction equation for this titration is
2S2O32- + I2 → S4O62- + 2I-
obviously we can't use our general formula (neither mA nor mB are constant). We have to use the general approach and assume that reaction went to (almost) completion.
We have to mix thiosulfate and iodine in 2:1 ratio. As solutions concentrations are identical that means we will use 2 volumes of thiosulfate and 1 volume of iodine, for the final volume of 3. Thus, taking both stoichiometry and dilution into account, we can write:
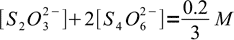 13
13and
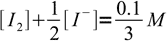 14
14However, reaction is shifted so far to the right, that concentrations of bot reactants are (in the mass balance) negligible:
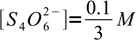 15
15and
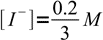 16
16We also know from the reaction stoichiometry that
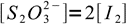 17
17Nernst equations for both systems are
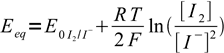 18
18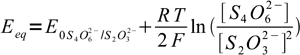 19
19Let's combine Nernst equations with known information listed above, aiming at removing all variables but [I2]:
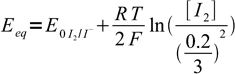 20
20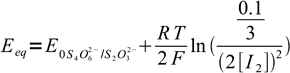 21
21We have two unknowns here. While we need Eeq, it is easier to calculate concentration of iodine first. Besides, that'll let us check if our assumption about the low iodine concentration was right. Subtracting second equation from the first one we get:
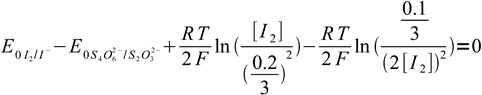 22
22After some rearranging and canceling:
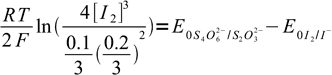 23
23or
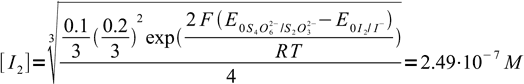 24
24as iodide concentrations was 0.2/3 = 0.0667 our assumption that I2 concentration is much lower was correct. Entering known concentration into Nernst equation we get
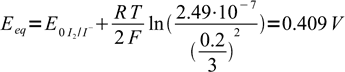 25
25and this is our equivalence potential. Note, that using derived formula we would get 0.308 V, almost 0.1 V off.




