Titration results calculation
Calculation of titration result is always based on the stoichiometry of the titration reaction.
When titrating we are usually given information about the volume and the concentration of the titrant solution and about volume of the titrated substance solution. Balanced reaction equation shows ratio of number of moles of reacting substances, thus to be able to deal with titration results we have to be able to convert between volumes, concentrations and numbers of moles. All these conversions are based on the definition of a molar concentration:
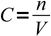 1
1which can be rearranged to calculate number of moles when concentration and volume are given:
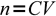 2
2(where n is number of moles, C concentration and V is volume).
In most cases concentration is given in moles per liter of solution (molarity, denoted here as M), but sometimes it can be also given as normality. For details see molarity and normality lectures on the ChemBuddy site.
For example let's look at the simple acid base titration - determination of concentration of sulfuric acid with the use of NaOH solution of known concentration CNaOH.
From the titration we know volume of titrant used (VNaOH).
We know that one mole of H2SO4 reacts with exactly two moles of NaOH:
2NaOH + H2SO4 → Na2SO4 + 2H2O
As we know that amount of substance of a given concentration in given volume of solution is C×V, and sulfuric acid reacts with sodium hydroxide in the 1:2 ratio, we can write:
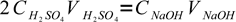 3
3There is only one unknown in this equation:
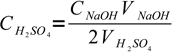 4
4Occasionally some additional calculations are needed, as determination of concentration of titrated substance may be only a step in the assay. For example if we are asked to find a purity of the substance, we must convert concentration found to amount of substance in the original sample. These calculations are usually based on simple number of moles/mass of substance conversions, or on simple dilution calculations.
10.00 mL sample of concentrated HCl was diluted to mark in 250 mL volumetric flask. To titrate 25.0 mL sample of diluted solution 43.56 mL of 0.1023 M NaOH was needed. What was the original concentration of hydrochloric acid?
We start with the reaction equation:
HCl + NaOH → NaCl + H2O
One mole of hydrochloric acid reacts with one mole of NaOH. For titration 0.04356 L×0.1023 M=4.456×10-3 mole of base was used, so there was 4.456 mmole of hydrochloric acid in every 25.00 mL of solution taken from the volumetric flask. Volumetric flask is 10 times larger than the samples titrated, so it contained 44.56 mmole of acid. This amount was originally found in 10.00 mL of concentrated acid - so original concentration was 44.56 mmole/10.00 mL=4.456 M (note that concentrations expressed in mmole/mL and mol/L have always the same numerical value, so to convert between them it is enough to change units).
1.456 g sample of unknown alloy was dissolved in acid and diluted to 100 mL. What was the percentage of iron in the sample, if titration of 20.00 mL aliquot of the diluted solution requires on average 33.45 mL of 0.01005 M solution of potassium permanganate?
As usual, we will start with the reaction equation:
5Fe2+ + MnO4- + 8H+ → 5Fe3+ + Mn2+ + 4H2O
33.45 mL of 0.01005 M solution of potassium permanganate contains 0.03345 L×0.01005 M=3.362×10-4 moles of titrant. Iron reacts with permanganate in 5:1 ratio, so 20.00 mL aliquot contains 5×3.362×10-4=1.681×10-3 moles of iron. There were exactly five such aliquots (100.00 mL vs 20.00 mL), so amount of iron in the sample was 5×1.681×10-3=8.404×10-3 moles, or 55.854 g/mol×8.404×10-3 mol=0.4693 g. That in turn means there was 0.4693 g/1.456 g×100%=32.23% iron in the sample.
1.354 g sample of sodium nitrate contaminated with NaCl was dissolved in small amount of water and filled to the mark in the 100 mL volumetric flask. To titrate chlorides in 10.00 mL sample 35.70 mL of 0.01021 M AgNO3 was used. What is the percent purity of the sample?
NaCl + AgNO3 → AgCl + NaNO3
Chlorides react with silver nitrate solution in 1:1 ratio. That means that 10.00 mL of chlorides solution contained 35.70×0.01021=0.3645 mmole of chlorides. Total sample was 10 times larger, so it contained 3.645 mmole, or 0.2130g (molar mass of NaCl being 58.33 g/mol). Sample contains 0.2130×100%/1.354=15.73% NaCl and 100%-15.73%=84.27% of sodium nitrate (assuming there are no other impurities).
Such calculations are rarely really difficult, but they are always time consuming. To make them much easier you may use EBAS - Equation Balancer And Stoichiometry calculator. You may download it from ChemBuddy site and we will provide ready files with reaction equations for all assays described.





