Complexometric titration - equivalence point calculation
At equivalence point we have just a solution of complex, and calculation of concentration of the ion is very similar to the precipitation titration case, we just have to account for the complex concentration. For that we have to know formation constant and complex stoichiometry. We could derive a formula similar to that derived in precipitation titration section, but as it was already signalled its use will be very limited. Most chelating reagents are weak acids and/or bases, so you quite often have to account for pH and speciation of ligand forms.
What is pAg at the equivalence point if the 0.01 M solution of cyanide is titrated with AgNO3 solution? Assume pH is so high CN- hydrolysis can be neglected, ignore dilution effects. log Kf = 21.1.
First of all - please note, that we are asked to calculate not concentration of titrated substance, but concentration of titrant (Ag+). Second, in the Liebig-Dénigès method of cyanides determination (which the question asks about), titrated solution is alkalized with ammonia, so the pH is high and assumption about lack of the hydrolysis is close to the reality.
Equation of the complexation reaction is
Ag+ + 2CN- → Ag(CN)2-
and the formation constant is
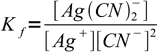 1
1At the equivalence point there are stoichiometric amounts of metal and ligans mixed so solution doesn't differ from the one prepared just by dissolving complex - and that means that
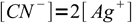 2
2so formation constant can be written as
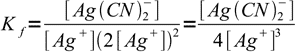 3
3This can be easily solved for [Ag+]. However, to calculate concentration of Ag+ we need one additional assumption - that Ag(CN)2- concentration can be treated as constant. Formation constant is relatively high, so this assumption is probably correct - but we will check it once we calculate Ag+ concentration.
As is obvious from the stoichiometry of the reaction, concentration of the complex is half that of initial cyanide concentration (in the real experiment it would be even lower, but we were asked to ignore dilution effects).
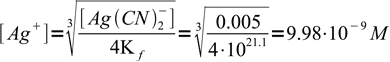 4
4and finally
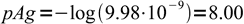 5
5It is time to check if our assumption was correct. Seems it was. Concentration of silver is 2×10-6 that of the complex concentration, which means we can safely ignore changes of the complex dissociation due to its dissociation.
What is pZn at equivalence point if 0.005 M ZnCl2 solution is titrated with 0.01 M solution of EDTA at pH 10? Complex formation constant log Kf = 16.8, pKa1=2.07, pKa2=2.75, pKa3=6.24, pKa4=10.34.
At the equivalence point we have just a solution of complex ZnEDTA2-. Complex dissociates according to the reaction
ZnEDTA2- → Zn2+ + EDTA4-
and the formation constant is
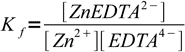 6
6Problem is, EDTA4- is a weak acid. Once the complex dissociates, ligand reacts with water, its concentration goes down and complex dissociates further. To be able to calculate concentration of Zn2+ we have to account for EDTA4- hydrolyzis.
How to do it? Let's start taking a look at given pKa values. We know that when pH=pKa concentrations of acid and conjugate base are identical. When pH changes by one unit, ratio of concentrations changes tenfold. That means that we can safely ignore pKa1, pKa2 and pKa3 - pH is so high concentrations of these acids will be neglectfully low. But what about pKa4?
This one can be not ignored, we are just 0.34 pH unit below. Let's take a look at acid dissociation constant:
 7
7After some rearranging (very similar to that used when deriving Henderson-Hasselbalch equation) this equation takes form
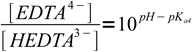 8
8which allows easy calculation of ratio of concentrations of acid and conjugate base. Note, that the same equation can be used for any acid.
From the stoichiometry and mass balance we also know that concentration of Zn2+ present in the solution must be identical to sum of concentrations of both EDTA4- and HEDTA3-:
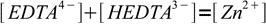 9
9We can easily get rid of [HEDTA3-] - it can be expressed in terms of known pH, pKa4 and yet unknown [EDTA4-]:
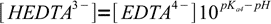 10
10(notice sign change in exponent) and substituted into mass balance:
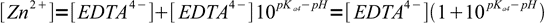 11
11or
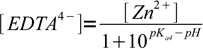 12
12Combined with complex formation constant:
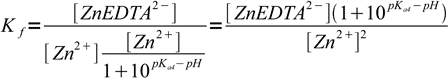 13
13In general we should also account for the fact, that some amount of ZnEDTA2- complex dissociated, but we won't - formation constant is high enough so that we can treat [ZnEDTA2-] as constant. To be sure we will check correctness of the assumption in the final step of calculations.
Solving for [Zn2+]:
 14
14The only thing we need now is the equivalence point concentration of ZnEDTA2- complex. We started with 0.005 M solution of Zn2+ and 0.01 M solution of EDTA. As these substances react 1:1 to each VZn we had to add VZn/2 of EDTA solution (compare concentrations if you don't know why), final volume is 1.5VZn and complex concentration is 0.005VZn/1.5VZn. Combining this concentration with pH and equation derived above, we get
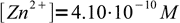 15
15and
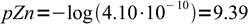 16
16Finally, we should check if our assumption that concentration of the complex can be treated as constant is valid - and it obviously is, as concentration of dissociation products is about 8 orders of magnitude lower.




