Titration curves calculation
While details of titration curve calculation depend on the titrant and titrated substance, general idea is always the same. There are three parts of titration curve - before equivalence point, equivalence point and after equivalence point.
Titration curve before equivalence point
Before end point we assume reaction was stoichiometric, went to completion (with titrant being the limiting reagent) and equilibrium state is defined by the concentrations of unreacted titrated system and products of the reaction.
Let's take a look at titrated systems at 50% titration.
In the case of strong acid titrated with strong base at 50% titration exactly half of the acid was neutralized and pH is simply minus logarithm of the left acid concentration (after taking account of the dilution, if necessary).
In the case of weak acid we have to deal with buffer and its pH is given by Henderson-Hasselbalch equation, thus pH at 50% titration equals acid pKa. In the case of redox titration we assume half of the titrated substance reacted, we use this assumption to calculate concentrations of reduced and oxidized forms of the substance and we enter these concentrations into the Nernst equation. Thus in the case of Fe2+ titration with any oxidizing agent at 50% titration potential of the system should equal formal potential of Fe2+/Fe3+ half cell (both Fe2+/Fe3+ concentrations are identical thus they cancel out in the reaction quotient, that's not necessarily case for other redox systems). In the case of both complexometric and precipitation titrations at 50% exactly half of the determined substance is in the original form while the other half is in the form of complex or solid.
Equivalence point
At the equivalence point calculations are based on the fact that there were stoichiometric amounts of titrant and titrated substance mixed in the solution. Thus for example in the case of acid-base titrations pH at the equivalence point is just a pH of salt solution (neutral for salt of strong acid and base, not neutral in the case of salts of weak acids or weak bases, as they undergo hydrolyzis). Concentration of ions at the equivalence point of precipitation titration is identical with concentration of ions in equilibrium with the weakly soluble salt and is calculated from the solubility product - and so on. Equivalence point calculations will be discussed in details in the appropriate sections.
Titration curve after equivalence point
After equivalence point titration curve shape is calculated from the excess of the titrant added - thus it will be just pH of excess titrant in the case of acid-base titration. In the case of complexometric titration we will calculate concentration of metal ions from formation constant, assuming all metal is complexed and the complexing agent concentration is just that of excess added.
Very close to the equivalence point
This part of the titration curve is usually the most difficult, as most approximations that work well for other parts of the curve may fail here. For example for strong acid-base titration we should account for two sources of the H+ ions - titrant (or titrated substance) and water auto dissociation (see pH of strong acid at ChemBuddy site for details). In general there is no easy method for titration curve calculation close to the equivalence point and we may be forced to use a most general approach to chemical equilibrium and solve a full set of equations describing the solution.
Dilution effects
To be precise in the calculations of titration curve we should take dilutions into account. Usually dilution effects are neglected, which is equivalent to the assumption that we use infinite concentration of titrant. That's not true, but in most cases titrated sample volume is three or four times larger than titrant volume and the dilution effects are small enough to be neglected.
Let's assume we are titrating strong monoprotic acid of initial volume Va0 and initial concentration Ca0 with strong monoprotic base of Cb concentration. We will use titration fraction, defined as ratio of acid neutralized to initial amount of acid, to express the titration progress.
At the beginning pH=-log(Ca0). After p fraction of the acid was titrated 1-p is left and new acid concentration is given by
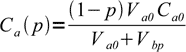 1
1Vbp, volume of base used to reach p, can be calculated from
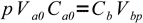 2
2(we have assumed both acid and base are monoprotic, thus all we have to do is to compare numbers of moles). So
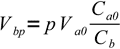 3
3and finally
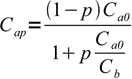 4
4Assuming we have started with 100 mL of 0.03 M acid and we use 0.2 M base pH at 50% titration is 1.82 (-log(0.015)) if we neglect dilution or 1.86 if dilution is taken into account. Difference is so small that we can safely ignore dilution effects. That's not always the case, if we will titrate 0.3 M strong acid pH will be either 0.83 (no dilution) or 1.07 (dilution taken into account). However, it is a standard procedure to use diluted titrated substance in volume of solution, and much more concentrated titrant, so usually when calculating titration curve we will be much closer to the first case.


