Acid base titration - end point indicators
Before proceeding with the end point detection discussion we should learn a little bit about the pH indicators behavior.
All pH indicators used for acid-base titration end point detection are weak acids or bases, with acidic form differing in color from the conjugate base. For now let's assume both forms have visible color - that doesn't have to be true, but we will discuss one color indicators separately. Indicator dissociation can be described by the reaction equation:
HInd ↔ H+ + Ind-
Let's call its acid dissociation constant KInd:
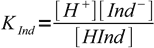 1
1This equation can be easily rearranged to important form, showing ratio of concentrations of both forms of the indicator:
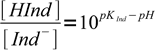 2
2Observed color of an indicator is a mixture of colors of both forms. At pH=pKInd both forms concentrations are identical (pH-pKInd=0, 100 = 1). When pH is one unit below pKInd, concentration of HInd is 10 times higher than concentration of Ind-, when pH is one unit above pKInd - concentration of HInd is 10 times smaller than concentration of Ind-.
If you will consult pH indicator table you will notice that in most cases it lists about 2 pH units distance between pure colors of an indicator. That's because for most hues sensitivity of human eye is too low to differentiate between colors of solution containing less then 10% of one form of the indicator. Note that this is an individual thing and ranges reported by different researchers for different indicators can differ. It is also possible that particular indicator has more forms and more close dissociation steps, in which case color change can be observed over wider pH range.
As pH indicators are weak acids (or bases), they have to react with titrant - and they will modifiy titration result. Luckily amount of indicators used are so small, that in most cases they can be safely ignored. For example phenolphthalein is used as 0.5% ethanol solution. We usually add about 2-3 drops of this solution to titrated sample. Assuming 20 drops per millilter, density of the solution 0.8 g/mL and molar mass of phenolphthaleine of 318 g/mol, we can calculate amount of added weak acid to be about 2×10-6 mole. As amount of titrated acids will be usuallly in the millimoles range, added micromoles of indicator can be safely ignored.
In the case of one color indicators we should take into account not only pKInd, but also total concentration of the indicator. Let's assume we have indicator HInd, dissociating according to the reaction
HInd ↔ H+ + Ind-
and Ind- is the visible form. Sum of concentrations of both forms is
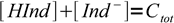 3
3which is just a mass balance equation. Combining above equations we can write
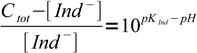 4
4If we know experimentally determined Ind- concentration Cvis, at which Ind- starts to be visible in the solution, we can regroup the equation to form:
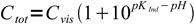 5
5That means that for every pH we can calculate total concentration of the indicator at which Ind- form will be visible. Let's try for phenolphthalein, for which Cvis is about 10-6 M and pKa=9.75 (phenolphthalein dissociation equilibria in the solution is multistage, but we can ignore other dissociation steps, as they occur at relatively distant pH values):
| solution pH | phenolphthalein Ctot |
|---|---|
| 6.0 | 5.6×10-3 M |
| 7.0 | 5.6×10-4 M |
| 8.0 | 5.7×10-5 M |
| 9.0 | 6.6×10-6 M |
| 10.0 | 1.6×10-6 M |
| 11.0 | 1.1×10-6 M |
Obviously regardless of pH we can calculate concentration at which we will be able to see pink tint. Note, that this is a border case concentration - for a given pH color will be visible for more concentrated solutions, but invisible for more diluted ones. Calculated values have practical limits, as phenolphthalein solubility in water is very low. We won't be able to prepare even 0.001M solution, nonetheless it is obvious that when dealing with one color indicators we can't ignore their concentration.
Same equation, solved for pH, can be used to calculate pH at which color change starts to be visible depending on the total indicator concentration.
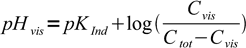 6
6Both pKInd and log(Cvis) are constant for a given indicator. Thus we can combine them into some new constant - let's call it pHvis0:
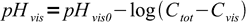 7
7As expected, for the indicator HInd pH at which color of Ind- starts to be visible goes down with increasing total concentration of the indicator. When Cvis is small comparable with Ctot:
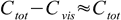 8
8and change of pH will be 0.3 unit per each twofold increase of Ctot:
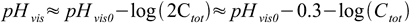 9
9When Cvis is too large to be ignored concentration dependent change of pHvis will be smaller.
Discussion above assumes pKInd is constant and doesn't depend on the solution ionic strength, thus pH changes always occur at the same pH. That's not the case. For low ionic strengths we can use following simplified equations:
| dissociation reaction | modified pK'Ind |
|---|---|
| HInd+ ↔ H+ + Ind | 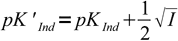 10 10 |
| HInd ↔ H+ + Ind- | 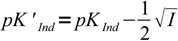 11 11 |
| HInd- ↔ H+ + Ind2- | 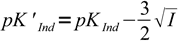 12 12 |
These equations can be easily derived using the most simplified version of the Debye-Hückel equation.
For IS=0.5 shifts in pKa can be in the 0.35 pH unit range.
pKInd also changes with temperature, and for example:
| indicator | color change range | |
|---|---|---|
| 18°C | 100°C | |
| thymol blue | 1.2-2.8 | 1.2-2.6 |
| methyl orange | 3.1-4.4 | 2.5-3.7 |
| methyl red | 4.4-6.2 | 4.0-6.0 |
| phenolphthalein | 8.2-9.8 | 8.1-9.0 |
Quoted from Chemia analityczna, J.Minczewski Z.Marczenko, PWN, Warszawa 1973.
Note that above discussion - while aimed at pH indicators - will be very similar in the case of complexometric indicators. Also main conclusions about problems at lower concentrations are universal and hold regardles on the titration type.





