Potentiometric titration - titration curve calculation

As usual, there are three parts of the curve. Before equivalence point we assume reaction went to completion according to the reaction equation - and we use concentrations of both oxidized and reduced forms of titrated substance to calculate the potential. At equivalence point we use one of methods described on the potentiometric equivalence point calculation page. Finally after the equivalence point we assume that concentration of reacted form of the titrant is that given by the reaction stoichiometry and concentration of the unreacted form is that of added excess - and we use these concentrations in Nernst equation.

Example: what is potential in 0.01 M Fe³⁺ solution titrated 25% with 0.0112 M Ti³⁺? E_{0Fe³⁺/Fe²⁺} = 0.77 V, E_{0Ti⁴⁺/Ti³⁺} = 0.130 V.

This is reduction titration, in which Fe³⁺ is being reduced to Fe²⁺:

Fe³⁺ + Ti³⁺ → Fe²⁺ + Ti⁴⁺

Using approach described above we can immediately write

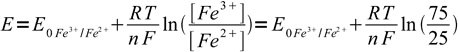1

as we know that already 25% of the iron is in the reduced form and so 100%-25%=75% have to be still in the oxidized form. We don't have to care about dilution factor, as it is identical for both forms of iron and cancels out. n is 1. Thus

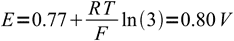2

Example: what is potential in 0.1 M H₂O₂ pH = 1.00 solution titrated 120% with 0.1 M permanganate? E_0O2/H2O2 = 0.682 V, E_{0MnO4^-/Mn²⁺} = 1.51 V.

In this titration hydrogen peroxide is oxidized by permanganate to water and oxygen:

5H₂O₂ + 2 MnO₄^- + 6H⁺ → 8H₂O + 5O₂ + 2 Mn²⁺

However, this reaction is irrelevant to the question. At 120% solution contains some amount of Mn²⁺ and 20% of that amount of excess permanganate. As both MnO₄^- and Mn²⁺ are present in the reaction quotient in the first power, their real concentrations don't matter, we are interested in the ratio only - and, similarly to the first question, we know enough to calculate this ratio as 20/100.

Nernst equation for the permanganate half reaction is

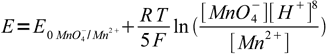3

From pH value we know H⁺ concentration is 0.1 M:

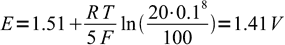4